The exponential decay of information

One of the major challenges of geology is the increasing sparsity of information about increasingly older times in Earth's history. This presents difficulties both when one is investigating a particular era, and when one is interested in looking at the frequency of events through time, or the frequency of rare events in general.

For example, we know close to infinitely more about the Holocene than the Precambrian, though the Precambrian was about 4 million times longer.

I think of this information loss as more or less exponential: basically that the total amount of available information for some geologic event or time period decays with time, similarly to radioactive Thedecay.

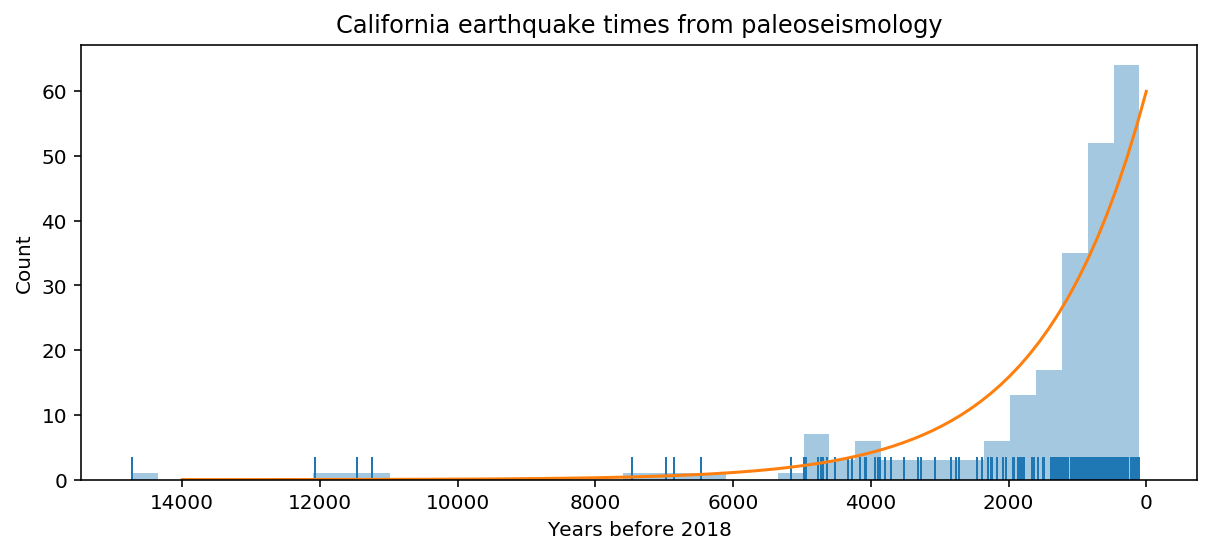
For example, I am playing around with paleoseismic data from California that was compiled as part of the UCERF3 effort (the data are available here). My main interest is whether there is any interdependence between the various faults, but a major confounding factor is that the data density drops off rapidly with time, meaning that we don't have complete records of surface-breaking earthquakes for much of the past, or even the past few thousand years (which is about the mean recurrence time for some of the slower faults).

Figure 1: Histogram of known of paleoearthquakes with time over the past ~15,000 years in California. Bin width is 500 years.

This decay in the rate of known earthquakes is something like an exponential. In this plot, I made an eyeball fit of an exponential decay curve that more or less matches the histgram bins:

This curve has a decay constant of 1/1500, or that a given earthquake rupture has a 50% probability of being lost (eroded, buried or otherwise obscured) every 1040 years, or an annual probability of being lost at about 0.00046 (or about 0.05%).

This isn't an exact fit: It's a little low in both the short and the long terms, and a little high in the medium term, but it gets the point across.

We tend to use a log scaling for how we perceive many quantities, including time (both forward and backward). An exponential decrease in information away from the present fits that nicely (Borges' Funes the Memorious reminds us that information and perception of time are linked). This is bidirectional as well, but as with out perceptions, the decay constants don't have to be equal. For the future, information surely decays faster.

An important note here is that information decay isn't fundamentally a physical process, in that information itself isn't. We could perhaps term it as knowledge. Though earthquake ruptures do become eroded, buried, and obscured through time, our knowledge of the past earthquakes can grow with time through effort. Just a handful of these events which occurred historically were known before paleoseismology.